A Taxonomy of Music
Nov 29, 2019 00:00 · 4385 words · 21 minute read
When I was a teenager getting into music, I came across Ishkur’s Guide to Electronic Music, which is1 a Flash application that gives relationships between (and audio samples from) several sub-genres of electronic music. I spent a lot of time listening to different snippets and trying to find MP3s on Audiogalaxy and Napster.
Ishkur’s guide has two major issues. First: it’s opinionated. With any sort of genre taxonomy, people like me come around to nitpick this or that relationship. Some of the genres listed don’t even appear to be real (‘Buttrock Goa’). Being a numbers guy, I prefer a more data-driven approach. The other issue is that Ishkur doesn’t scale. Making the guide must have been very labor intensive. There are so many new releases and so many new genres that its hard for one person to keep up with them. Theres a reason that he took over a decade off from it. In the course of putting this together, I did find that theres a new “v3” guide released this year.
What I’d like to do is put together something algorithmically that automates and addresses those issues. Doing this might take some of the heart out of a project like Ishkur’s, but I think we can get to a point where we have pretty reasonable relationships between genres, while allowing us to expand beyond electronic music.
Discogs
A great data source for this project is Discogs. It’s a website for organizing your music collection. All the information is crowdsourced, and they take correctness very seriously (every time I log in feel like I have 50 messages notifying me of small changes to something in my collection). And best of all, because it’s all community contributed Discogs provides the data under a CC0 (no rights reserved) license.
Each release on Discogs gets tagged with some content information. Genres are broad strokes groupings (e.g. ‘Hip-Hop’, ‘Rock’, ‘Jazz’), and styles which are more fine-grained subgenres (e.g. ‘Indie Rock’, ‘Contemporary R&B’, ‘Synth Pop’). Styles don’t belong to a genre so there’s some cross-over: there are albums with the genre tag ‘Electronic’ and the style tag ‘Lo-fi’, for example2.
Albums are reissued and remastered all the time, different markets can have slightly different tracklists, and so on. Discogs organizes these into master releases, that all the different versions correspond to. That’s the data we’ll be working with. Discogs has just over 1.5 million master releases in the November 2019 data release.
What I’d like to do is use the fuzzyness of these labels to identify similar genres and styles. Styles that are often tagged together should be more similar to one another than ones that arent. Releases that are tagged with ‘Big Band’ are also often tagged with ‘Swing’, so they should be similar genres. ‘Hardcore’ and ‘Jazz-Funk’ don’t get tagged together often, so they’re probably not that similar. That’s not to say someone couldn’t somehow bridge those styles together. It’s just that doing that is difficult so there would be fewer releases with both styles.
Quantifying Similarity
So we’ve got the idea that similar things are tagged together more often. How do we turn that into a number? That’s not necessarily straightforward. There’s a huge number of similarity and dissimilarity measures out there. This paper compares 76 of them. This one also covers many of the same measures.
I worked through the dataset to identify all releases associated with a genre/style. A given release can be either present in both genres, present in one but not the other, or present in neither. The table below describes the situations, with \(a\), \(b\), \(c\), and \(d\) as the number of releases in each given configuration.
| Present in Genre A | Absent from Genre A | Totals | |
|---|---|---|---|
| Present in Genre B | \(a\) | \(b\) | \(a+b\) |
| Absent from Genre B | \(c\) | \(d\) | \(c+d\) |
| Totals | \(a+c\) | \(b+d\) | \(n=a+b+c+d\) |
I’m not going to work through and evaluate over 70 semi-redundant similarity measures. I’ve chosen out the following few as my potential measures. They’re all expressed in terms of \(a\), \(b\), \(c\), and \(d\).
| Measure | Formula | Range |
|---|---|---|
| Jaccard | \(\frac{a}{a+b+c}\) | [0,1] |
| Cosine | \(\frac{a}{\sqrt{(a+b)(a+c)}}\) | [0,1] |
| Yule’s \(Q\) | \(\frac{ad-bc}{ad+bc}\) | [-1, 1] |
| Simple Matching Coefficient (SMC) | \(\frac{a+d}{a+b+c+d}\) | [0, 1] |
| Russel-Rao | \(\frac{a}{a+b+c+d}\) | [0, 1] |
It’s important that the dissimilarity measure makes decisions that make sense to us. There’s an important role for domain expertise in any analysis. The styles ‘Ambient’ and ‘Drone’ should be similar. So should ‘Sludge Metal’ and ‘Doom Metal’. ‘Country’ and ‘Country Rock’ should be very close. ‘Folk’ and ‘Noise’ should be pretty far. World music from distant cultures should be far. ‘Downtempo’ and ‘Speed Metal’ should be extremely far. Our similarity/dissimilarity measure should reflect these.
I picked a couple style pairings to evaluate the performance of the measures. Genres are too fuzzy for this task, I think I could spin an answer out of any similarity score I got. Styles are specific enough that I can say “that makes sense” or “not a chance”. Performance of each similarity measure on my style pairs are shown below.
| Style A | Style B | Expected | Jaccard | Cosine | Yule | SMC | Russel-Rao |
|---|---|---|---|---|---|---|---|
| Ambient | Drone | Close | 0.153 | 0.323 | 0.944 | 0.951 | 0.009 |
| Barbershop | Vocal | Close | \(5.8 \times 10^{-4}\) | 0.017 | 0.910 | 0.955 | \(2.6 \times 10^{-5}\) |
| Synthwave | Vaporwave | Close | 0.032 | 0.061 | 0.936 | 0.996 | \(1.4 \times 10^{-4}\) |
| Country | Country Rock | Close | 0.072 | 0.135 | 0.875 | 0.979 | 0.002 |
| Sludge Metal | Doom Metal | Close | 0.121 | 0.265 | 0.983 | 0.990 | \(1.3 \times 10^{-4}\) |
| Hardstyle | Trance | Far | 0.006 | 0.028 | 0.643 | 0.970 | \(1.9 \times 10^{-4}\) |
| Indie Rock | Industrial | Far | 0.005 | 0.011 | -0.541 | 0.932 | \(3.5 \times 10^{-6}\) |
| Math Rock | Ska | Far | \(1.7 \times 10^{-3}\) | \(3.7 \times 10^{-4}\) | -0.837 | 0.991 | \(1.5 \times 10^{-6}\) |
| Polka | Quechua | Far | \(1.7 \times 10^{-3}\) | 0.006 | 0.858 | 0.998 | \(3.1 \times 10^{-4}\) |
| Smooth Jazz | Free Jazz | Far | 0.002 | 0.004 | -0.010 | 0.991 | \(2.0 \times 10^{-5}\) |
| Thrash | Zydeco | Far | 0 | 0 | -1 | 0.988 | 0 |
I tried several measures and they mostly became swamped by the sheer size of the dataset. There are a lot of styles and genres, and for any two of them the \(d\) term is going to be massive. As a result, SMC and Russel-Rao are basically useless. SMC is greater than 95% in all cases, and Russel-Rao is almost uniformly near zero. Jaccard isn’t doing great either. Cosine similarity \(S_{cos} = \frac{a}{\sqrt{(a+b)(a+c)}}\) showed some promise, but the range was was small. Cosine also whiffed on Barbershop/Vocal, Synthwave/Vaporwave and Country/Country Rock.
Given the size of the dataset, and the number of styles, its clear in retrospect that \(a\) is not enough to drive our similarity metric, leading to the performance issues of Jaccard and Cosine. Measures based on simple addition can’t cope with the size of \(d\), which is always going to be massive, compared to \(a\), \(b\), and \(c\).
Yule’s \(Q\) gives pretty intuitive results (despite placing Quechua and Polka close together). This might be because its a measure that focuses on the relationship of \(a\) and \(d\) to the \(b\) and \(c\) terms, rather than just trying to scale \(a\) against the non-shared releases. Conventiently for me, \(Q\) is also expressable as a dissimilaritry (\(D_{YuleQ} = \frac{2bc}{ad+bc}\))3. One rub, though is that \(Q\) requires \(d\), which is a bit of an inconvenience, because we have to keep track of which releases are in neither of the sets of releases we’re considering. If we have \(n\) though, we can calculate \(d=n-a-b-c\).
Genre Similarity
Releases on discogs are grouped into 15 genres, which again are pretty broad and somewhat nebulous (Synth-pop is obviously Pop but is it Electronic? Is it Rock?).
One way to visualize dissimilarities is with a dendrogram. I’ve built this one from R’s hclust hierarchical clustering. You read a dendrogram from the bottom up: close items will join each other toward the bottom of the tree. As you move up to the top of the tree, more distantly related things join together, until finally all the items are joined together and the whole dataset is together. This was put togther with average linkage: clusters join together with clusters that have the lowest average dissimilarity from them. There are other linkage approaches but this one worked best in practice.

Rock is close to blues, and both are close to Pop which makes sense historically. As does Funk/Soul, Reggae, Electronic, and Hip-Hop going together. I’d have expected Stage & Screen to be closer to classical, but I wasn’t considering the amount of Broadway soundtracks and the like.
Style Similarity
We did genres, but what about styles? There are a lot more styles than genres, and most don’t have many releases associated with them.

It’s too difficult to interpret a dendrogram with over 500 styles. So let’s restrict to releases with over 10,000 releases.

This dissimilarity measure is definitely working for us. I think most of the relationships here make sense: Punk/Hardcore, Garage Rock/Psychedelic Rock, Folk/Folk Rock/Acoustic, Synth-pop/New Wave are all very natural groupings. This group of top styles does somewhat show the bias of the dataset: Discogs is primarily a site focusing on electronic music and rock, so Jazz and Classical aren’t really represented in the top styles list.
I’d like to visualize all the styles though, so a dendrogram won’t cut it. What we have now is a dissimilarity matrix (which we can pretend is a distance matrix4), but these distances don’t correspond to any particular locations. One way to get positions corresponding to the distances is UMAP. UMAP makes some very mathy assumptions (that datapoints are uniformly distributed on a Riemannian manifold) and uses our distances to find low-dimensional positions.
What’s useful about UMAP in our scenario is that it tries to resolve positions locally. It’s not super-important to me that ‘Mambo’ and ‘Tech House’ are precisely the right distance from each other. They’re very unrelated styles. What’s important is that the distance between the individual Jazz styles or the individual Metal styles are right. UMAP makes its embedding based on the nearest points. The broader structure will work itself out from there. For this analysis I’ve set UMAP to look at the 25 closest styles.
I also used the clustering above to find clusters of releases, to see how the two approaches agree and disagree. There will be disagreements. I arbitrarily picked 10 clusters.
Let’s plot our UMAP styles. I’ve excluded styles with less than 100 releases, leaving us with 415 styles remaining. I’m still not going to be able to fit every style on one plot, but I’ve added a lot of ‘signposts’ to let you see the lay of the land.
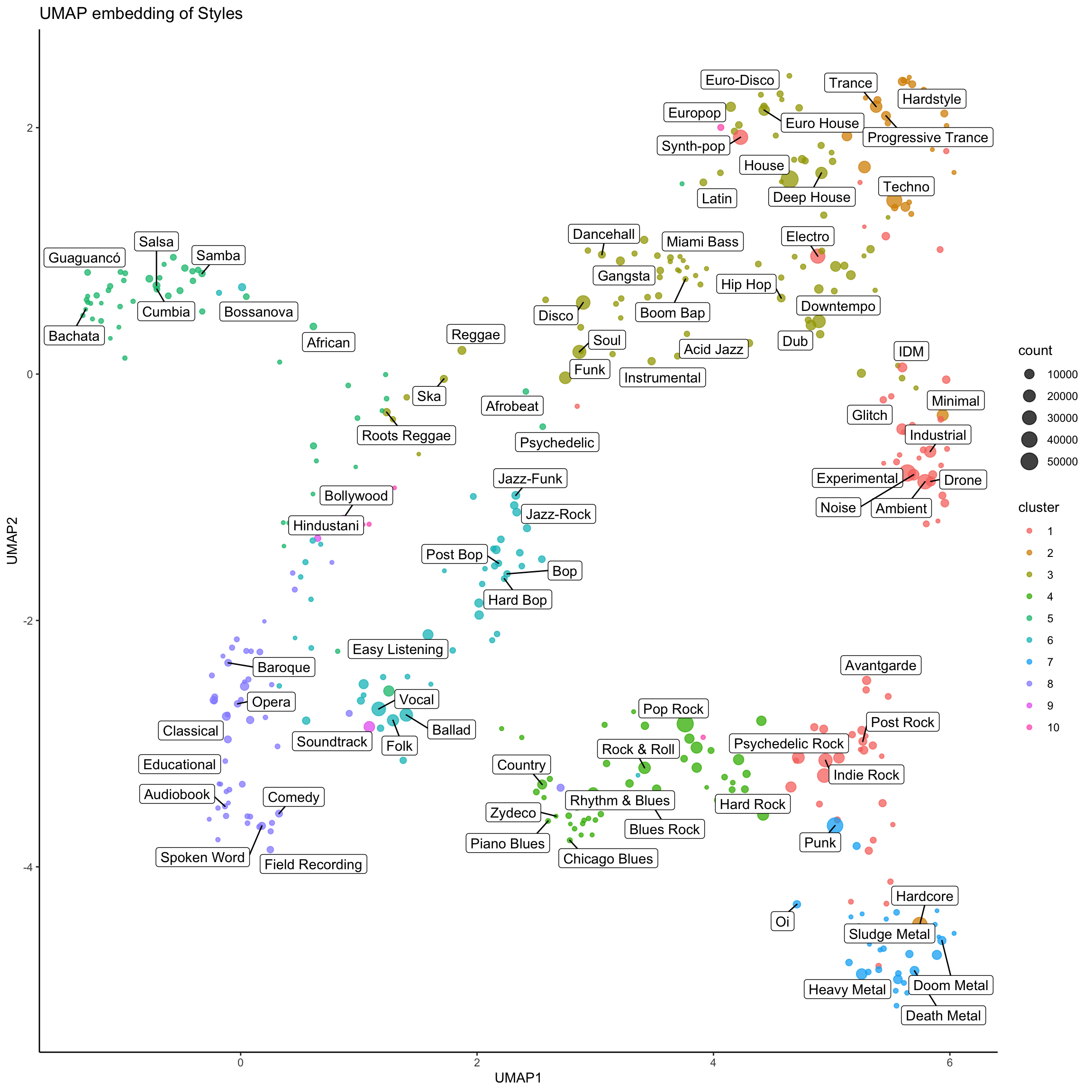
This seems like a pretty good embedding, and it also mostly agrees with the clustering. The places where they differ are interesting. UMAP as ‘Hardcore’ with punk and metal styles, but the clustering puts it with electronic music. Hardcore appears as a style in both ‘Electronic’ and ‘Rock’ genres, with different meanings. Each algorithm picked up on different meanings. Cluster 9 only has ‘Hindustani’, ‘Bollywood’ and ‘Soundtrack’, which seems fair enough. Clustering places ‘Reggaeton’ with latin styles, but UMAP holds it closer to the electronic ones. Cluster 1 runs up the UMAP2 axis from ‘Nu-metal’ in the bottom, through ‘Alternative Rock’ and ‘Indie Rock’. Then it continues into the ‘Darker’ electronic genres like ‘Industrial’, ‘IDM’, ‘EBM’. Finally it reaches the top of the plot with ‘Electroclash’ and ‘Synthpop’. Cluster 1 is a very 90s/Early 2000s set of styles.
Implementation
I’d generally leave data wrangling out of my posts but I decided to get all this data into shape in Spark, and there’s basically no examples of real-world Spark programs that are easy to find. Every example is the ‘count the words in a file’ from the Spark documentation. This analysis didn’t need Spark (again, I’m doing it on a 2016 Macbook Pro), but it’s easy to express the required data manipulation in it.
XML Extraction
Happily, Discogs makes all this data available as a gzipped well-formed XML file. The problem is that there’s enough data that trying to build parse the entire tree on my MacBook causes me to run out of memory. Python’s built-in XML ElementTree parser will let you lazily handle a huge file, but the documentation doesn’t make it particularly obvious how to do it.
Our XML is structured like this (with some tags and information we don’t need omitted):
<masters>
<master id="57416">
<main_release>1678659</main_release>
<images>
<image height="600" type="primary" uri="" uri150="" width="593"/>
...
</images>
<artists>
<artist>
<id>3225</id>
<name>Vince Watson</name>
...
</artist>
</artists>
<genres>
<genre>Electronic</genre>
</genres>
<styles>
<style>Techno</style>
</styles>
<year>1996</year>
<title>Tuff Trax #1 - Basic Functions</title>
<data_quality>Correct</data_quality>
</master>
...
</masters>
If you naively use ElementTree.parse() it will try to build the entire data structure in one go and you’ll run out of memory and your computer will grind to a halt. An alternative method is ElementTree.iterparse(). This is a generator that emits the XML tags and events (e.g. ‘start of tag’, ‘end of tag’) as it gets to them. Now you can process the file as you go through it. When you get an ‘end’ event from iterparse, you can work with the tag as if it were a normal XML element5.
If you naively use ElementTree.iterparse() it will also try to build the entire data structure and you’ll run out of memory and your computer will grind to a halt. It’s not lazily going over it like a generator, it’s just letting you know whats going on as you build the tree. What you can do, though, is modify the tree as you’re building it. In this code I grab the root node of the element tree (the first one parsed out of the file), and after every master release I process, I call clear() on the root node to erase what’s in the tree.
import gzip
import xml.etree.ElementTree as et
# outer_delimiter separates release id, genres, and styles
# inner_delimiter separates individual genres and styles
outer_delimiter, inner_delimiter = '\t', '|'
def get_info(node):
"Returns genres and styles for a discogs master release"
genres_node, styles_node = node.find('genres'), node.find('styles')
genres = ([g.text for g in genres_node.findall('genre')]
if genres_node else [])
styles = ([s.text for s in styles_node.findall('style')]
if styles_node else [])
return genres, styles
def delimit(seq, delim):
"Clearer helper function for delimiting sequences"
return delim.join(str(x) for x in seq)
with gzip.open(input_filename) as xml_file:
root = None
for event, element in et.iterparse(xml_file, events=('start', 'end')):
# This is ugly but it lets us keep track of the
# root node
if root is None:
root = element
if event == 'end' and element.tag == 'master':
release_id = element.attrib['id']
genres, styles = get_info(element)
print(release_id,
delimit(genres, inner_delimiter),
delimit(styles, inner_delimiter),
sep=outer_delimiter)
# Clear the root so that it doesn't keep the data we've already
# processed in memory.
root.clear()Now we have we have our data in a more useful format. We only have the data we need: master release IDs, genres, and styles. This is a plain text file, and the three fields are delimited by a tab. Genres and styles can have multiple values, so they’re delimited with a pipe.
229069 Electronic Techno|Minimal|Tech House 229134 Electronic Techno 229474 Rock Thrash|Stoner Rock|Heavy Metal 229556 Electronic House|Downtempo 229960 Electronic|Rock House|Electro|Indie Rock|Disco
Processing with pySpark
So now what I have is releases with styles attached to them. What I actually want is the reverse: styles with releases attached to them. The reason this feels natural6 to me in Spark is that, because of its distributed nature, you can just “shake out” all the styles-release pairs into a pile and put them back together the way you want. Like sorting socks.
If you’re familiar with Python’s list comprehensions or generator expressions, you’ve got most of what you need to understand working with Spark RDD’s on a basic level. Let’s sum up the squares of even numbers below 100 with a python generator expression: sum(x**2 for x in range(100) if x % 2 == 0). This expression is doing a couple things here. The x**2 for x in range(100) is the map component. We’re applying a transformation to every element in range(100). This doesn’t have to be a small expression either, f(x) for x in q is valid for any function f. The next part, if x % 2 == 0 is the filter component. As we’re going through range(100), we’re only keeping values of x that don’t have a remainder when divided by two. The function sum is a reducing function: it takes every element in a sequence and applies a function as it goes through. In this case that function is simple addition. Finally notice that this is a generator expression: ignoring the call to sum() for a second, we are performing these transformations when we need the result. You can do a lot with just these three concepts7.
Spark lets you process large datasets in parallel on multiple cores (and computers) if you program this way. It does this via the Resilient Distributed Dataset (RDD) API. Spark distributes the data across its workers. RDD’s are resilient in the sense that that Spark keeps track of what data it sends where, and if one of the worker nodes dies it can regenerate it. With an RDD we can use map, filter, and a few other functions to define transformations on a dataset. Then when we either need the data (or need to compute a reducing function on the data), Spark distributes the data and computes it.
Analysis of genres and styles are basically the same, so I’ll only present styles here.
Our first step is to parse our input text file. You could accomplish this by a lot of small anonymous lambda functions8 (this is what most Spark tutorials do), but writing out a slightly bigger function with a name helps with code clarity.
# Creating the named tuple lets us make code a little clearer
from collections import namedtuple
Release = namedtuple('Release', ['release_id', 'genres', 'styles'])
def process_line(item):
toks = item.strip().split(outer_delimiter)
release_id = toks[0]
genres_styles = [set(x.split(inner_delimiter)) for x in toks[1:]]
# Some releases may not have styles or genres attached. If they have a
# style but not a genre, we'll still have a regular 3-tuple. If they don't
# have either we'll need add empty collections for both.
while len(genres_styles) < 2:
genres_styles.append([])
return Release(release_id, genres_styles[0], genres_styles[1])The next set is to ‘dump’ out all these genres and styles into a pile. The function unnest_styles ‘flattens’ the styles and genres9. For example data that looks like [('release_a', ['genre'], ['style_a', 'style_b']), ('release_b', ['genre'], ['style_b', 'style_c'])] will be transformed to [('release_a', 'style_a'), ('release_a', 'style_b'), ('release_b', 'style_b'), ('release_b', 'style_c')]. Now that we have release-style pairs, we can use invert_kvp to invert the key-value pair so that ('229134', 'Techno') becomes ('Techno', '229134'). Now that it’s in that form, Spark will collect everything corresponding to the key for us.
def unnest_styles(item):
release, genres, styles = item
for style in styles:
yield release, style
def invert_kvp(kvp):
key, value = kvp
return value, keyCertain RDD functions work with keys. They treat each item in the dataset as a key-value pair, and use that key to let you work on subsets of the data, like a GROUP BY clause in SQL. For example countByKey is the equivalent of the SQL query SELECT key, count(*) FROM [table] GROUP BY key. The RDD function combineByKey lets us make collections out of all of the items corresponding to a key. The first one makes a collection out of an item. For our purposes, we need to make a set containing just one item. The next argument adds an item to an existing collection. And the last merges two collections together. Because Spark RDDs immutable, these functions should return new objects, not modify existing objects. For example, set.add doesn’t work here, because, while it adds items to a set, it doesn’t return a value.
# Collection creator
def create_set(item):
return set([item])
# Add to a collection
def add_to_set(current_set, new_item):
return set.union(current_set, create_set(new_item))
# Merge two collections
def join_sets(set_a, set_b):
return set.union(set_a, set_b)We need functions to compute the Yule’s \(Q\) dissimilarity. yuleq(a,b) computes this for two sets a and b (naturally). The function compute_distances_with_sample_size wraps yuleq, transforming the data as it comes out of the RDD into \(a\), \(b\), \(c\) and \(d\). Since distance metrics are symmetric (\(D(a,b) = D(b,a)\)), compute_distances returns them both.
def yuleq(a, b, c, d):
return (2 * b * c) / (a * d + b* c)
def compute_distances_with_sample_size(pair, n):
"Helper function to compute distance"
# pair is a tuple in the form:
# ((style_name, [releases]), (style_name, [releases]))
kvp1, kvp2 = pair
key1, values1 = kvp1
key2, values2 = kvp2
if key1 == key2:
score = 0.0
else:
a = len(values1 & values2)
b = len(values1 - values2)
c = len(values2 - values1)
d = n - (a + b + c)
score = yuleq(a, b, c, d)
yield key1, key2, score
yield key2, key1, scoreNow we’re ready to build an RDD. Lets build one that gives each style and the corresponding releases. You can tell the current Spark Context (sc) to read a file line by line with textFile(). We’ve already written all our important functions, so now it’s just a matter of combining them. map() applies a function to every element in the RDD. flatMap() is similar, but allows the number of elements in the RDD to change. filter() only keeps elements that evaluate to True by a specified function. We’ve already discussed combineByKey() above.
lines = sc.textFile('genres_styles.txt')
style_releases = (
lines.map(process_line)
.filter(lambda x: len(x.styles) > 1)
.flatMap(unnest_styles)
.map(invert_kvp)
.combineByKey(create_set,
add_to_set,
join_sets)
)At this point we haven’t done anything. The RDD we’ve made here only describes the steps we’ll use to get what we want. It’s a recipe, but not the meal. This will only turn into data when we tell Spark to go get it. We can use collect() to completely execute the RDD (If you only need a subset take() will also give you a user-specified number of records). Certain ‘reducing’ functions (sum, max, etc.) will also cause Spark to go evaluate an RDD. In my code I also call persist() at the end of the RDD creation to force Spark to hang on to the results from the RDD because I use it a couple times.
The last step is computing the distances. We already created the distance functions before, we just need to evaluate it for every pair of styles. The RDD method cartesian() produces each possible combination of values from two RDDs. Evaluating style_releases.cartesian(style_releases) gives every combination of items in style_releases. Since we wrote compute_distances to exploit the symmetry of distances, we filter out half of the pairs.
style_distances = (style_releases.cartesian(style_releases)
.filter(lambda x: x[0] < x[1])
.flatMap(compute_distances))
style_distances_evalutated = style_distances.collect()Now style_distances_evaluated has all the data we wanted. It’s a list in the format [('style_a', 'style_b', dist) ...], and we write it to disk in whatever format is convenient to us. I picked a ‘melted’ csv.
Things that didn’t work
Can’t pretend that everything works perfect on the first try!
- Dendrograms were created with “average” linkage in hierarchical clustering. Average linkage feels like the right approach for this problem, and other linkage choices didn’t give as good results.
- I tried other embeddings besides metric MDS, but MDS was still the best choice. Old classics are classics for a reason.
- MDS embedding was okay, but there were some odd features from a ‘sanity check’ point of view. ‘Punk’ is pretty far from ‘Hardcore’, which itself was strangely close to ‘Minimal’. ‘Comedy’ was between ‘Classical’ and ‘Blues Rock’.
- I attemped nonmetric MDS with a couple different R packages (
MASS,vegan,smacof), but they never converged, only bouncing around a local optimum. When I looked at where it was hovering, it wasnt a good embedding. - The MDS algorithm as implemented in
smacofallows you to specify a weight matrix. I tried weighting the dissimilarities between two styles as the smaller of the number of releases of the two styles. The embedding I found this way was definitely different but not much more compelling than what you get without doing that. - Embedding with Isomap (as implemented in
vegan), gave different embeddings but they didn’t appear to make much sense. - After tuning, tSNE (as implemented in
scikit-learn) gave basically the same embedding as UMAP: a big doughnut with offshoots for Latin styles and Metal styles. There’s not really a benefit to tSNE over UMAP, and tSNE’s ‘perplexity’ hyperparameter is less straightforward than UMAP’s number of neighbors.
- Other similarity/dissimilarty measures were evaluated, but didnt make the cut for an already long blog post. I also looked at Gower, Stiles, Dice, and \(a\) and \(a+d\) directly.
I was genuinely surprised that the original Ishkur’s guide is still online.↩︎
Their section for the genre ‘Funk/Soul’ with the style ‘Modal’ doesn’t include Nujabes’ Modal Soul, which would have been cute.↩︎
If you’re looking up \(Q\) note that scipy had an issue for a while where their documentation had the wrong formula.↩︎
Yule is not a proper metric to my knowledge, so it’s not quite right to call this a dissimilarity. This paper on comparing top-\(k\) lists shows that Goodman & Kruskal’s \(\gamma\) statistic fails the triangle inequality. Yule’s \(Q\) is a special case of \(\gamma\) when applied to binary variables. I’m not aware if the specialness of the case provides a stronger guarantee.↩︎
Only after you reach ‘end’ is the full
Elementfully structured. If you only need the tag attributes, you can look at ‘start’.↩︎‘Natural’ in the sense that it’s easily implemented once you understand Spark. Spark will do all the work that I don’t want to do.↩︎
These ideas are from functional programming. Python provides
mapandfilteras built-ins. With the move to Python 3reducehas been moved to thefunctoolslibrary, which contains several other useful functional programming utilities likepartial,wraps, andlru_cache.functoolsis part of the standard Python distribution↩︎Python
lambdaexpressions let you assign short functions to variables instead of having to use full definitions. For examplef = lambda x: x**2is equivalent todef f(x): return x**2. Python does have the restriction that lambda statements can only be expressions. They’re most useful as anonymous functions: short functions we can create on the fly. For example, we can pass a function to the functionsortedand use that to determine the order of the sorting:sorted(our_list, key=lambda x: x[1])lets you sort by the second value of every item inour_list.↩︎It’s called ‘unnest’ in reference to the function in Google BigQuery that does the same thing.↩︎